Kisházi gondolatok

Specifikáció

Kötelező megérteni, és pontosan követni. Ha spec megjegyzést találsz a hf értékelésben, akkor ezt nem tetted meg.

Indentálás (befogazás(?), tabulálás)

A kód vizuális struktúrájának tükröznie kell az algoritmikus szerkezetet. Enélkül olvashatatlan, rosszabb esetben félreérthető a kód (csak az embernek, a compilernek mindegy). A helytelenül, vagy nem indentált feladatokat mostantól nem fogom bogarászni. (Mellékesen: mind a VC, mind a code::blocks automatikusan helyesen indentál, illetve bármikor kérhetünk újraformázást.)

Órai dolgok

Az órán téglalap (és kör) osztályt készítünk. A kör osztály annyiban különbözik a téglalaptól, hogy írunk egy setr(double); tagfüggvényt is. A kör osztály kerület- és területszámító függvényeinek szükségük van π értékére. Egyik lehetőség egy globális const double pi=3.14…; definiálása.

Ennél kultúráltabb megoldás a matematikai headerben általában definiált M_PI makró konstans használata (nem szabványos elem). Ez gcc alatt helyből elérhető, m$vc alatt trükközni kell, némely régebbi compilerben esetleg egyáltalán nincs definiálva. A követendő kódolás:

#define _USE_MATH_DEFINES	//M$VC igényli
#include <cmath>		//C++-ban, C-ben math.h
#ifndef M_PI			//ha nincs ilyen, akkor se érjen meglepetés
const double pi=3.14159265358979323846;
#else
const double pi=M_PI;
#endif

Gyakorlófeladatok:

1. Általános kétdimenziós vektor	2. Nemnegatív koordinátájú kétdimenziós vektor
3. Hallgatók adatainak nyilvántartása	4. Téglatest osztály
5. Mátrix osztály	6. Háromdimenziós vektor osztály
7. Egész Bignum	8. Tank osztály
9. Tört osztály	10. Multihalmaz osztály

4. Házi feladat.

1. Írjunk egy háromszög osztályt, az alábbiak szerint:
   • Az osztály kívülről hozzáférhetetlenül tárolja a háromszög három oldalát! A háromszög egyéb adatait (pl. szögeit) nem szabad tárolni!
   • Inicializáláskor a háromszöget meg lehessen adni két oldalával és a közbezárt szöggel, két szögével és közéjük eső oldalával, illetve három oldalával, de valamelyiket mindig meg kell adnunk, kezdeti argumentum nélkül ne lehessen példányosítani. Azt, hogy melyik kombinációt adtuk meg, azt egy negyedik, enum típusú paraméterrel adjuk meg. (Most a ctor lesz a leghosszabb tagfüggvény, a definícója kerülhet a .cpp-be)
   • Gondoskodjunk róla, hogy a háromszög inicializálás után mindig korrekt értékeket tartalmazzon, még esetleges ügyetlen/hibás felhasználás esetén is. Negatív oldalak/szögek megadása esetén használjuk az adat abszolút értékét. Ha a szög(ek) nagysága (összege) nem jó, vagy a három oldalból nem lehet zárt alakzatot alkotni, helyette egységoldalú szabályosat kell létrehozni.
   • A későbbiekben a háromszög adatait nem módosítjuk. (Nincs set() fv.)
   • A háromszög bármely alapadata (három oldal ill. szög) lekérdezhető legyen.
   • Legyen egy kiíró tagfüggvény, mely a 6 alapadatot írja ki. (Más tagfüggvény nem ír ki.)
   • Ezen túl az osztály képes legyen kiszámolni a háromszög területét, kerületét és megállapítani, hogy derékszögű-e (±1% pontossággal tekintsük annak). Ez utóbbit úgy kell megvalósítani, hogy igen nagy és igen kicsi oldalhosszak esetén is helyesen működjön. A területszámításhoz a Hérón-képlet használatát ajánlom.
     
     
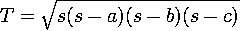
   • A program tagolása a C++ programozók körében elterjedt konvenciók alapján történjen (.h: osztálydeklaráció, .cpp: hosszabb implementációjú függvények törzse), és védjük ki a többszörös beépítésből eredő újradefinicióról szóló hibaüzeneteket. A tesztelő függvény (ld. alább) is külön állományba kerüljön.
   • Készítsünk egy tesztelő függvényt (main), amely mindhárom megadásnál jó és hibás adatokkal is teszteli a konstruktort és a többi tagfüggvényt.
   • Szorgalmi részfeladat: Írjunk egy osztályon kívüli diagnosztikai célú printer függvényt is, amely kiírja a tagváltozók értékét, és a tagfüggvények által visszaadott kerület, terület valamint derékszögűség értéket. (Ez a függvény, mivel nem része az osztálynak, kerüljön a tesztelővel egy file-ba.)